磁束密度 B [T又はWb/m2] の磁界とθの角度をなす長さ l [m]の導線に I [A]の電流が流れているとき,この電流が磁界から受ける力
F [N/m]は
F = NIBlsinθ [N/m]
N:巻数 方向は右ネジの法則に従います。
磁束密度 B [Wb/m2] の磁界と角度θをなす方向に速度 v [m/s]で運動している電気量 q [C]の荷電粒子があるとき、この荷電粒子が磁界から受ける力
F [N/m]は
F = q vBsinθ [N/m]
で、方向はフレミング左手の法則に従います。
真空中で距離r[m]隔てた磁極m [Wb] 間に働き合う力F[N/m]は
![]()
真空中で距離r[m]隔てた,無限に長い平行な直流電流I1 [A],I2 [A]の単位長さ1[m]あたりに働き合う力F[N/m]は
![]()
μo:真空の透磁率
電流I1,I2が同じ方向なら引力,反対方向なら斥力として働きます。
図のように磁束密度B=0.5[T]の一様な磁界の中に直線状の導体を磁界の方向に対して30°の角度におき、これにI=100[A]の直流電流を流した。このとき、導体の単位長さ当たりに働く力F[N/m]の値として、正しいのは次のうちどれか。
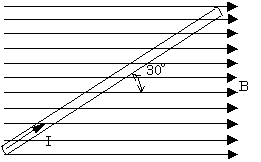
(1) 10 (2) 25 (3) 38 (4) 46 (5) 53]
答え (2)
電流が流れている導体を磁界中に置くと、フレミングの( ア )の法則に従う電磁力を受ける。これは導体中を移動している電子が磁界から力を受け、結果として導体に力が働くと考えられている。
また、強さが一定の一様な磁界中に、磁界の方向と直角に電子が突入した場合は、電子の運動方向と常に( イ )方向の力を受け、結果として等速( ウ )運動をすることになる。このような力を( エ )という。
上記の記述の空欄箇所( ア )、( イ )、( ウ )及び( エ )に記入する語句として、正しいものを組合せたのは次のうちどれか。
| ( ア ) | ( イ ) |
|
( エ ) | |
| (1) |
|
|
|
|
| (2) |
|
|
|
|
| (3) |
|
|
|
|
| (4) |
|
|
|
|
| (5) |
|
|
|
|
答え (1)
真空中において、同一平面内に、無限に長い3本の導体A、B、が互いに平行に置かれている。導体Aと導体Bの間隔は2[m]、導体Bと導体Cの間隔は1[m]である。
導体には図に示す向きに、それぞれ2[A]、3[A]、3[A]の直流電流が流れているものとする。このとき、導体Bが、導体Aに流れる電流と導体Cに流れる電流によって受ける1[m]当たりの力の大きさF[N/m]の値として、正しいのは次のうちどれか。
ただし、真空の透磁率をμ0=4π×10-7[H/m]とする。
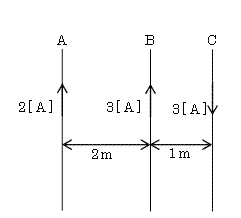
(1) 1.05×10-6 (2) 1.20×10-6 (3) 1.50×10-6
(4) 2.105×10-6 (5) 2.40×10-6
答え (5)



