交流とは時間変化に伴って、電圧や電流が変化する電源です。

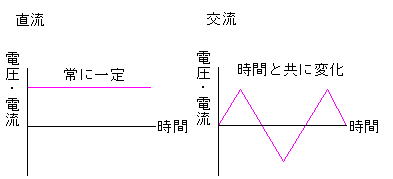
発電機によって作られた電気の波形を示したもので、純粋でひずみがなく全ての交流波形の基礎となります。

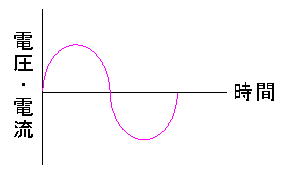
正弦波の表記にはｓｉｎ関数が用いられ、横軸をｘ、縦軸をyとすると

　ｙ　＝　sinｘ

の関係式が成り立ちます。このｓｉｎ関数を基本として、波形の特徴を表す量は

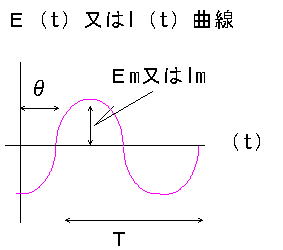
瞬時値　：　e（ｔ）[V]　、　i（ｔ）[Ａ]
最大値、振幅　：　Ｅm[Ｖ]　、　Ｉm[Ａ]
周期　：　Ｔ[ｓ]
周波数　：　ｆ[Ｈｚ]　　ｆ＝1/Ｔ
角速度、角周波数　：　ω[rad/ｓ]　ω＝２πｆ＝２π/T
位相　：　θ[rad]
が用いられ式で表すと

　ｅ（ｔ）　＝　Ｅｍｓｉｎ（ωｔ±θ）
　ｉ（ｔ）　＝　Ｉｍｓｉｎ（ωｔ±θ）

などと表されます。上式を図で表すと下図のようになります。

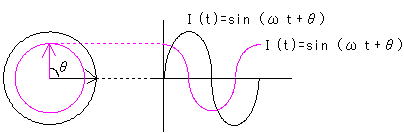
２つの波形の時間的なずれを位相差と言います。考え方としては対応する円を描き考えると解かり易いです。位相の遅れなら−、進みなら＋で表します。

ｅ（ｔ）＝Ｅｍｓｉｎ（ωｔ±θ）やｉ（ｔ）＝Ｉｍｓｉｎ（ωｔ±θ）は瞬時値の為、値が時間と共に変化し扱いが面倒となることから、計算に使うには平均値 Eav [V] 、 Iav [Ａ] や実効値 |Ｅ| [Ｖ]、 |Ｉ| [Ａ] を用います

平均値は波形１周期についての平均的な値のことで、絶対値をとり波形の面積を求め周期Ｔで割ります。最大値との関係式は
　Ｅav　＝　2/π×Ｅｍ　[Ｖ]
　Ｉav　＝　2/π×Iｍ　[Ａ]

実効値は実際に仕事をする交流電力の値のことです。同一の抵抗において直流の場合と同じ電力を消費する等価回路を表します。後々の計算に用いますのでよく理解しておきましょう。ちなみに家庭用のコンセントが100Ｖであるというのは、この実効値のことで、最大値は141.4Vとなります。最大値との関係式は
　|E|　＝　Em/√2[Ｖ]
　|Ｉ|　＝　Ｉm/√2[Ａ]

図1の回路において、図2のような波形の正弦波交流電圧v[V]を抵抗R=10[Ω]に加えたとき、流れる電流の瞬時値i[A]を表す式として、正しいのは次のうちどれか。ただし、電源の周波数を50[Hz]とする。

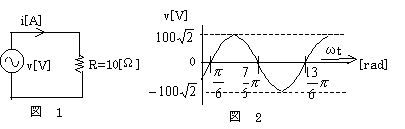
（１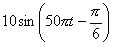）		（２）
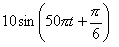（３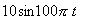）		（４）
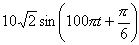（５）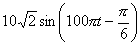

答え　（5）

ある回路に電圧(1式)を加えたところ。回路に(2式)の電流が流れた。この電圧と電流の位相差θ[rad]を時間[s]の単位に変換して表した値として、正しいのは次のうちどれか

（１）　1/400　　（２）　1/600　　（３）　1/1200　　（４）　1/1440　　（５）　1/2400

答え　（3）