導体が電荷を蓄える能力のことで、C [F]で表します。
![]()
Qは電荷 [C] : Vは電位差 [V]
平行平板コンデンサの静電容量
![]()
S:電極の面積 [㎡]、ε:誘電体の誘電率 [F/m]、εs:誘電体の比誘電率、εo:真空の誘電率8.85×10-12 [F/m]、d:コンデンサ間の距離 [m]
図のように、面積 S[㎡]の電極からなる平行板コンデンサがある。この電極板と平行に同じ形の導体平板を図に示す間隔で入れ、このコンデンサの両端の電極の電極に120[V]の直流電圧を加えて充電した。このとき、図中の電圧V0
[V]の値として、正しいのは次のうちどれか。
ただし、電極板間の誘電体の誘電率は同一とし、充電前の電極及び導体平板の初期電荷は零とする。また、電極板及び導体平板の厚さ並びにこれらの端効果は、無視できるものとする。
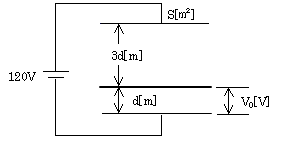
(1) 0 (2) 30 (3) 60 (4) 90 (5) 120
ヒント : 答え (2)
真空中において、一辺l[m]の正方形電極を間隔d[m]で配置した平行板コンデンサがある。図1はこのコンデンサの電極板間に比誘電率εr=3の誘電体を挿入した状態、図2は図1の誘電体を電極面積の1/2だけ引き出した状態を示している。図1及び図2の二つのコンデンサの静電容量C1[F]及びC2[F]の比(C1:C2)として、正しいのは次のうちどれか。
ただし、l>>dであり、コンデンサの端効果は無視できるものとする。
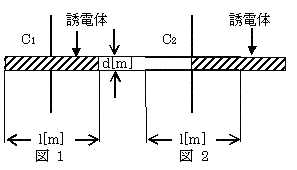
(1) 2:1 (2) 3:1 (3) 3:2 (4) 4:3 (5) 5:4
ヒント : 答え (3)
真空中において、面積S[m]2の電極板を間隔d[m]で配置した平行板コンデンサがある。この電極板と同じ形をした厚さ(d/2)[m]、比誘電率2の誘電体を図に示す間隔で平行に挿入した。このとき、誘電体を挿入する前と比較してコンデンサの静電容量[F]は何倍になるか。その倍率として最も近いのは次のうちどれか。
ただし、電極板の厚さ並びにコンデンサの端効果は、無視できるものとする。
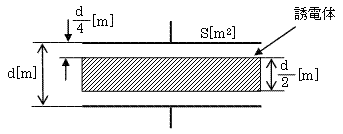
(1) 1.3 (2) 1.5 (3) 2.0 (4) 2.5 (5) 3.0
ヒント : 答え (1)



