静電界 ステップアップ問題
真空中において、それぞれ質量m[kg]、電荷+Q[C]の小さな球の帯電体A及びBがある。これらの帯電体をそれぞれ長さr[m]の糸で点Pからつるしたところ、図のように、帯電体A、Bの間隔がa[m]となって静止した。
次の(a)及び(b)に答よ。
ただし、真空の誘電率ε0[F/m]、重力加速度g[m/s2]とする。また、帯電体A及びBの直径はr[m]に比べて十分小さく、糸の質量は無視できるものとする。
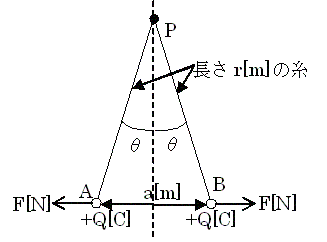
(a) 帯電体A、B間に働く力F[N]の大きさとして、正しいものは次のうちどれか。
| (1) | Q/(4πε0a) | (2) | Q/(4πε0a2) | (3) | Q2/(2πε0a) |
| (4) | Q2/(2πε0a2) | (5) | Q2/(4πε0a2) |
(b) 帯電体A、B間の静止状態において、糸の鉛直直線に対する傾きがθ°であったときに成立する式として、正しいのは次のうちどれか。
| (1) | Q2=16πε0mgr2(sin2θ)(tanθ) |
| (2) | Q2=16πε0mgr2(sin2θ)/(tanθ) |
| (3) | Q2=16πε0mgr2(cos3θ)/(sinθ) |
| (4) | Q2=8πε0mgr2(sin2θ)(tanθ) |
| (5) | Q2=8πε0mgr2(sinθ)(cosθ) |
答え (a)−(5)、(b)−(1)
電極板の間隔がd0[m]、電極板面積が十分に広い平行板空気コンデンサがある。このコンデンサの電極板間にこれと同形、同面積の厚さd1[m]、比誘電率εrの誘電体を図のように挿入した、いま。このコンデンサの電極A,Bに+Q[C],-Q[C]の電荷を与えた。次の(a)及び(b)に答よ。
ただし、コンデンサの初期電荷は零とし、端効果は無視できるものとする。また、空気の比誘電率は1とする。
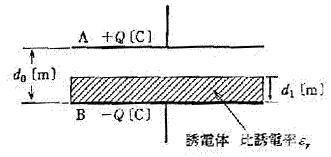
(a) 空げきの電界E1[V/m]と誘電体中の電界E2[V/m]の比E1[V/m]/E2[V/m]を表す式として、正しいものは次のうちどれか。
| (1) | εr | (2) | εrd1/(d0-d1) | (3) | εrd12/(d0-d1)2 |
| (4) | εr(d0-d1)/d1 | (5) | εrd1/d0 |
(b) 電極板の間隔d0=1.0×10-3[m]、誘電体の厚さd1=0.2×10-3[m]及び誘電体の比誘電率εr=0.5としたとき、空げきの電界E1=7×10-4[V/m]であった。
コンデンサの充電電圧V[V]の値として、正しいのは次のうちどれか。
(1) 100.8 (2) 70.0 (3) 67.2 (4) 58.8 (5) 56.7
答え (a)−(1)、(b)−(4)



