過渡現象とは直流回路にインダクタンスLやキャパシタンスCを接続し、スイッチを入れた瞬間や切った瞬間に電圧や電流が不安定な状態になる現象です。電圧や電流が落ち着いた状態を定常状態といい、不安定な状態を過渡状態と言います。
ＲとＣからなる回路では
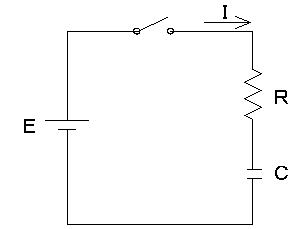
時刻ｔ における、コンデンサの電荷量Ｑ（ｔ）は
として表されまので、キルヒホッフの法則に当てはめると回路方程式
が成立します。（Ｑ＝ＣＶ）
この方程式を変換すると
コンデンサの過渡現象はこの
で決まり、ＣＲの積の事を、時定数Ｔと言います。単位には秒［ｓ］を用います。
Ｔ＝ＣＲ ［ｓ］
尚、インダクタンスＬの過渡現象は
で表され、時定数Ｔは
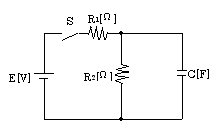
図の回路において、スイッチSを閉じた瞬間(時刻ｔ=0)に抵抗R1に流れる電流をI0[A]とする。また、スイッチSを閉じた後、回路が定常状態に達したとき、同じ抵抗R1に流れる電流I∞[A]とする。上記の電流I0及びI∞の値の組み合わせとして、正しいのは次のうちどれか。
ただし、コンデンサＣの初期電荷はゼロとする。
|
|
|
|
| （１） |  |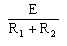
 |
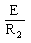| （２） |
 |
 |
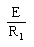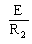| （３） |  |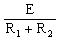
 |
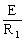| （４） |
 |
 |
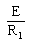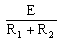| （５） |
 |
|
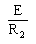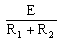答え （4）
図のように、抵抗RとインダクタンスLのコイルを直列に接続した回路がある。この回路において、スイッチSを時刻t=0で閉じた場合に流れる電流及び各素子の端子間電圧に関する記述として、誤っているのは次のうちどれか。
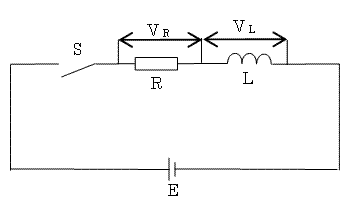
| （１） | この回路の時定数は、Lの値に比例している。 |
| （２） | Rの値を大きくするとこの回路の時定数は、小さくなる。 |
| （３） | スイッチSを閉じた瞬間(時刻t=0)のコイルの端子間電圧VLの大きさは、零である。 |
| （４） | 定常状態の電流は、Lの値に関係しない。 |
| （５） | 抵抗Rの端子間電圧VRの大きさは、定常状態では電源電圧Eの大きさに等しくなる。 |
答え （3）
問-9
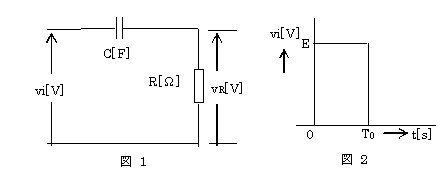
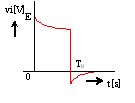
図1のような静電容量C[F]のコンデンサと抵抗R[Ω]の直列回路に、図2のような振幅E[V]、パルス幅T0[s]の方形波電圧vi[V]を加えたときの抵抗Rの端子間電圧vR[V]の波形(赤線)として、正しいのは次のうちどれか。
ただし、図1の回路の時定数RC[s]はT0[s]なり十分小さく(T0[s]>>RC)、電源の内部インピーダンス及びコンデンサの初期電荷は零とする。
| （１） |
 |
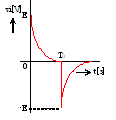（２） |
 |
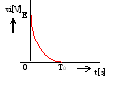| （３） |  |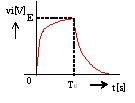
（４） |  |
| （５） |  |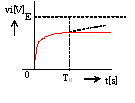
答え （１）
